최소 힙 / 최대 힙

2022.03.18 - 힙 트리 (Heap tree) 글에 이어서, 힙 트리에는 두 가지 종류가 존재한다.

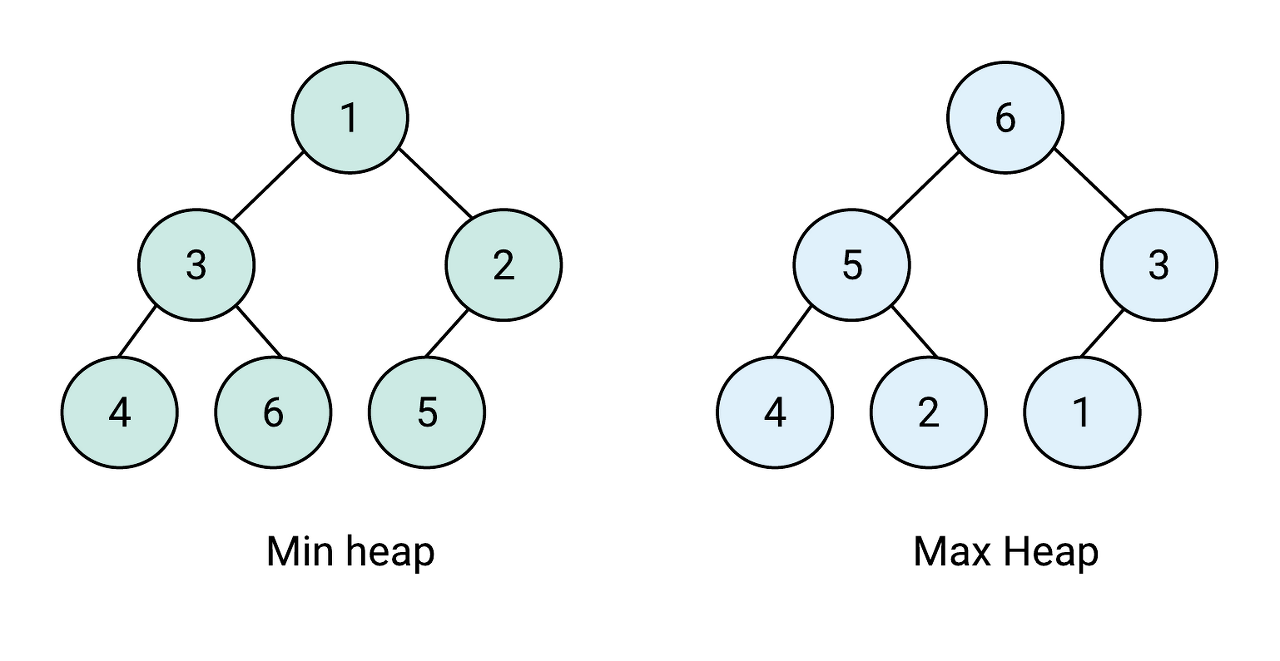
최소 힙 (Min heap) : 부모 노드가 자식 노드보다 작거나 같다.

최대 힙 (Max heap) : 부모 노드가 자식 노드보다 크거나 같다.

 

형제간에는 대소 관계가 없다.

최소 힙에서는 루트 노드가 최솟값이 되고 최대 힙에서는 루트 노드가 최댓값이 된다.

 

삽입 연산 

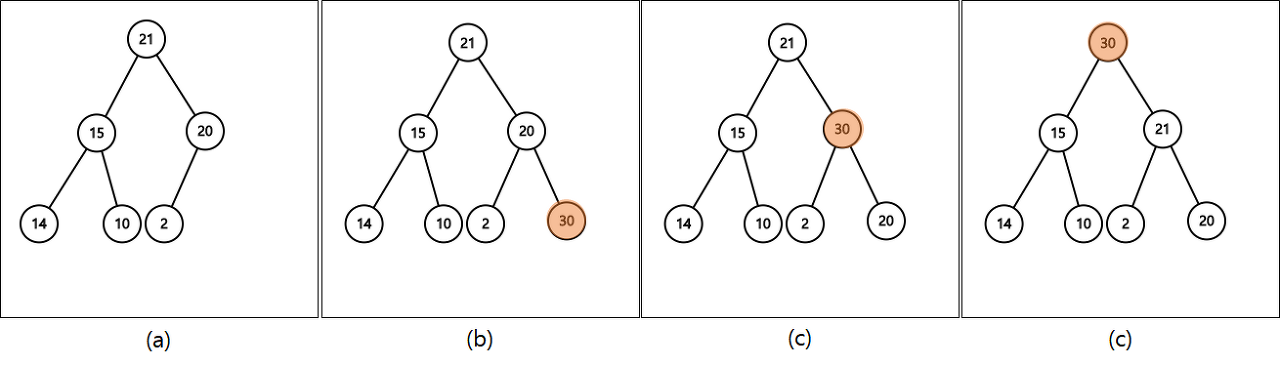
1. 트리 끝에 노드를 추가한다.
2. 부모 노드와 대소를 비교한다.
   최대 힙인 경우, 추가한 값이 부모 노드보다 크면 자리를 바꾼다.
   최소 힙인 경우, 추가한 값이 부모 노드보다 작으면 자리를 바꾼다.
3. 2번을 반복한다.

최대 힙에서의 삽입

 

코드

삽입 연산을 python 코드로 나타내면 아래와 같다.

def insert_h(heap, val):
    heap.append(val) # 배열에 값 추가
    t = len(heap) - 1
    while t >= 2 and heap[t] > heap[t // 2]: # 부모 노드가 자식 노드보다 커질 때까지 반복
        heap[t], heap[t // 2] = heap[t // 2], heap[t] # 부모 노드와 자식 노드 위치 바꿈
        t = t // 2

 

삭제 연산

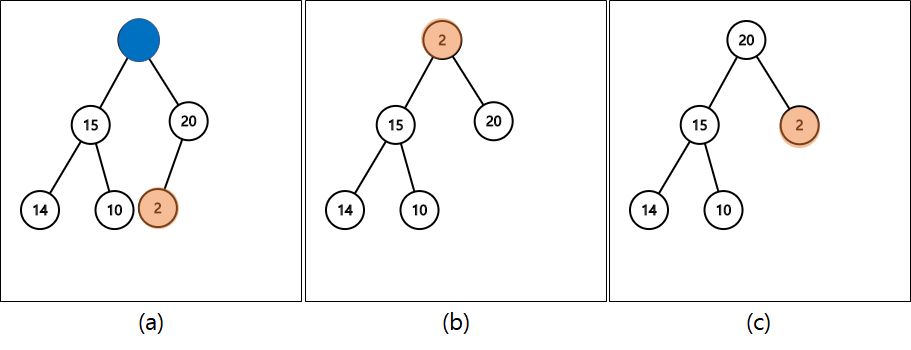
1. 루트 노드에서 값을 제거한다.
2. 마지막 노드를 루트 노드로 옮긴다.
3. 자식 노드와 대소관계를 비교한다.
   최소 힙인 경우, 자식 노드 중에서 더 작은 노드와 부모 노드의 자리를 바꾼다.
   최대 힙인 경우, 자식 노드 중에서 더 큰 노드와 부모 노드의 자리를 바꾼다.
4. 3번을 반복한다.

최대 힙에서의 삭제

코드

삭제 연산을 python 코드로 나타내면 아래와 같다.

def delete_h(heap):
    heap[1], heap[-1] = heap[-1], heap[1] # 루트 노드와 마지막 노드 자리 바꿈
    r = heap.pop(-1) # 기존 루트 노드 삭제
    t = 1
    while 2 * t + 1 < len(heap) and heap[t] < max(heap[2 * t], heap[2 * t + 1]): # 자식 노드보다 커질 때까지 반복
        if heap[2 * t] > heap[2 * t + 1]: # 자식 노드 중 더 작은 노드와 자리 변경
            heap[t], heap[2 * t] = heap[2 * t], heap[t]
            t = 2 * t
        else:
            heap[t], heap[2 * t + 1] = heap[2 * t + 1], heap[t]
            t = 2 * t + 1
    return r

 

시간 복잡도

힙은 최대 힙의 높이만큼 탐색하므로, O(logn)의 시간 복잡성을 가진다.