트리
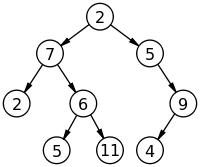
그래프(Graph)의 일종
스택이나 큐와 같은 선형 구조가 아닌 비선형 자료 구조이다. 계층적 관계를 표현한다.
cycle이 없고, 서로 다른 두 노드를 잇는 길이 하나인 그래프를 트리라고 한다.
특징
- 하나의 루트 노드(root node, 최상위 노드)를 갖는다.
- 노드 a가 노드 b를 가리킬 때, a를 b의 부모 노드(parent node)라고 한다. b는 a의 자식 노드(child node)라고 한다.
루트 노드는 0개 이상의 자식 노드를 갖는다. - 자식 노드는 0개 이상의 자식 노드를 갖는다.
자식 노드가 없는 노드는 잎 노드(leaf node)라고 한다. 잎 노드가 아닌 노드는 내부 노드(internal)라고 한다. - 자식 노드는 한 개의 부모 노드를 가진다.
- 노드와 노드를 연결한 길은 간선(edge)이라고 부른다.
- n개의 노드를 가진 트리는 n-1개의 간선을 가진다.
- 트리는 cycle이 존재하지 않는다. 시작 노드에서 출발해 다른 노드를 거쳐 다시 시작 노드로 돌아올 수 있다면 cycle이 존재하는 그래프에 해당한다.
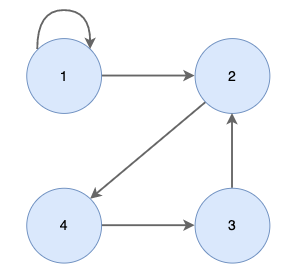
- 트리는 self-loop이 존재하지 않는다.
용어
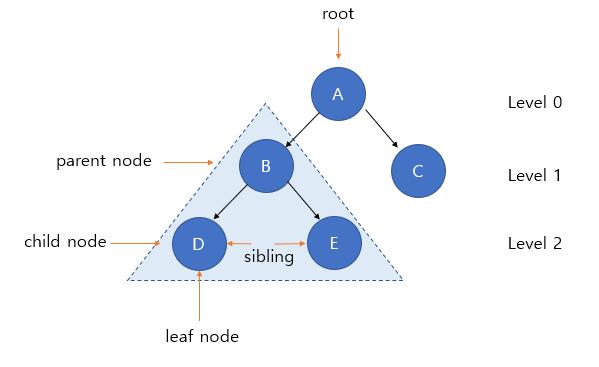
- 형제 (sibling) : 같은 부모 노드를 갖는 노드
- 경로 (path) : 한 노드에서 다른 한 노드에 이르는 길 사이에 있는 노드의 순서
- 길이 (length) : 한 노드에서 다른 한 노드까지 거치는 간선의 수
- 깊이 (depth) : 루트 노드에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
- 레벨 (level) : 트리의 특정 깊이를 가지는 노드의 집합
- 높이 (height) : 트리의 최대 깊이
- 차수 (degree) : 자식 노드의 개수
- 트리의 차수 (degree of tree) : 트리의 최대 차수
- 크기 (size) : 노드의 수
종류
이진 트리 (Binary Tree)
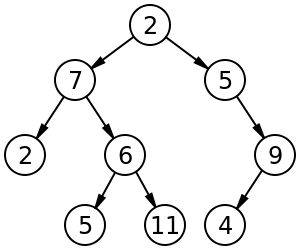
각 노드가 최대 두 개의 자식을 갖는다.
완전 이진 트리 (Complete Binary Tree)
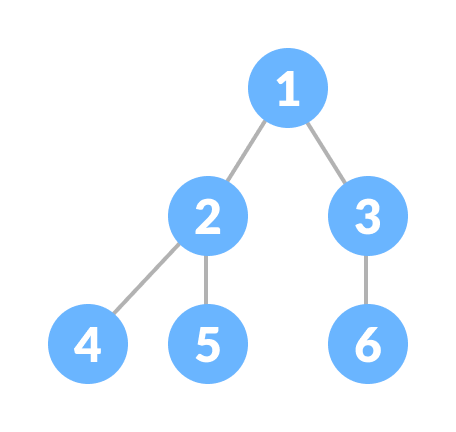
마지막 레벨을 제외한 모든 레벨이 채워져 있다.
마지막 레벨은 왼쪽부터 채워져 있다.
마지막 레벨 l는 1개부터 2*l-1 개의 노드를 가진다.
전 이진 트리 (Full Binary Tree)
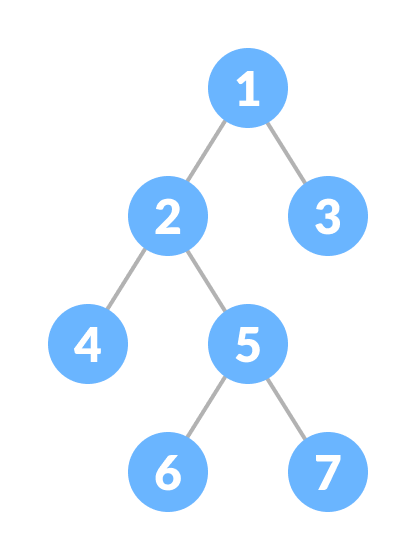
모든 노드가 0개 또는 2개의 자식 노드를 갖는다.
포화 이진 트리 (Perfect Binary Tree)
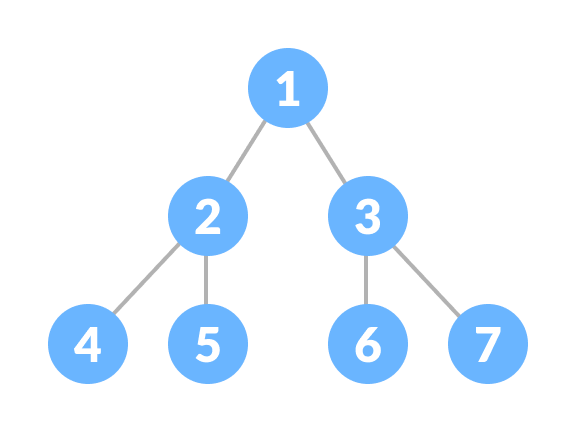
모든 레벨에 노드가 전부 채워져 있다.
모든 노드는 0개 또는 2개의 자식 노드를 갖는다.
모든 잎 노드는 동일한 깊이이다. 또한 동일한 레벨에 속한다.
트리의 노드 개수는 2^h-1이다. h는 트리의 높이에 해당한다.
이진 탐색 트리 (Binary Search Tree)
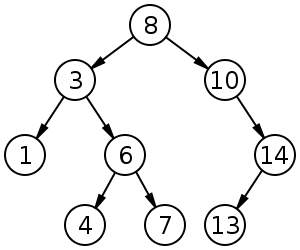
노드에 저장된 키는 유일하다.
부모의 키가 왼쪽 자식 노드의 키보다 크다.
부모의 키가 오른쪽 자식 노그의 키보다 작다.
왼쪽과 오른쪽 서브 트리도 이진 탐색 트리이다.
참고 문서
https://ko.wikipedia.org/wiki/%ED%8A%B8%EB%A6%AC_%EA%B5%AC%EC%A1%B0
728x90