힙 트리
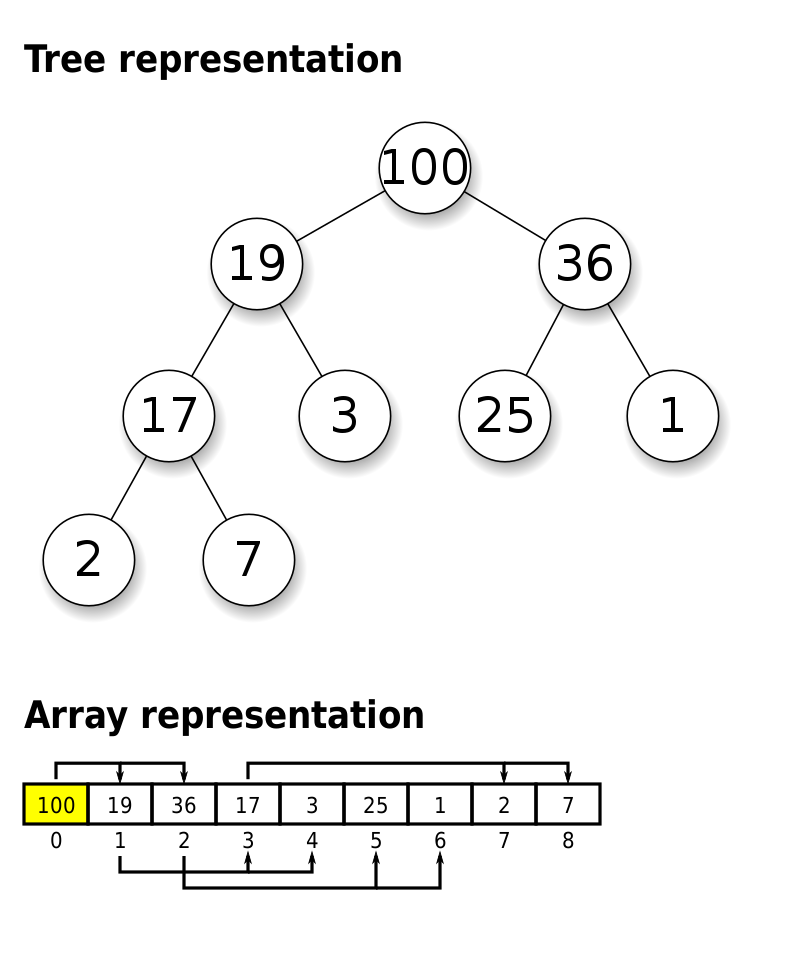
최댓값 또는 최솟값을 빠르게 찾기 위해 고안된 완전 이진트리의 일종
우선순위 큐를 위해 만들어진 자료구조이다.
부모-자식 노드 간의 대소관계가 성립한다는 속성을 만족하며, 일종의 반정렬 상태(느슨한 정렬 상태)를 유지한다. 형제 간의 대소 관계는 없다.
값을 중복하여 저장할 수 있으며, 일반적으로 간단히 heap이라고 말한다.
우선순위 큐
데이터가 우선순위를 가지고 있어, 우선순위가 높은 데이터가 먼저 나가는 우선순위의 개념을 큐에 도입한 자료 구조
배열, 연결 리스트 또는 힙으로 구현할 수 있으며 셋 중에서는 힙으로 구현하는 것이 가장 효율적이다.
구현
힙 트리는 1차원 배열로도 충분히 구현할 수 있다.
조건
- 루트 노드의 인덱스는 1이다. 0으로 설정하면 부모-자식 간의 대소관계를 표현하기 어렵다.
- 왼쪽 자식 노드의 인덱스 = 부모 노드 인덱스 * 2
- 오른쪽 자식 노드의 인덱스 = 부모 노드 인덱스 * 2 + 1
- 부모 노드의 인덱스 = 자식 노드 인덱스의 // 2 (여기서 //는 나눗셈의 몫을 뜻한다.)
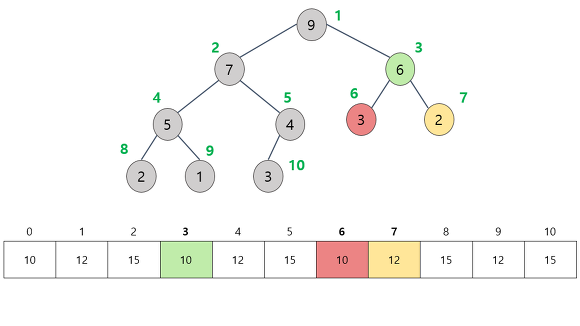
Heap에서 삽입 및 삭제 연산이 어떻게 이뤄지는지는 다음에 마저 정리한다.
참고 문서
https://mattlee.tistory.com/48
https://ko.wikipedia.org/wiki/%ED%9E%99_(%EC%9E%90%EB%A3%8C_%EA%B5%AC%EC%A1%B0)
728x90