문제
https://www.acmicpc.net/problem/2921
1. 두 칸으로 이루어진 도미노 조각이 있다. 각 칸에는 점이 찍혀 있을 수도 있고, 찍혀있지 않을 수도 있다.
2. 점의 개수는 세트의 크기에 의해 결정된다. 세트의 크기가 N인 도미노 세트에서 점의 개수는 0보다 크거나 같고, N보다 작거나 같다. (0 ≤ 점의 개수 ≤ N)
3. 두 개의 도미노 각 칸에 찍힌 점의 개수가 같으면, 두 도미노는 동일하다. 즉, 점이 2개, 8개 찍혀있는 도미노와 점이 8개, 2개 찍혀있는 도미노는 서로 같다.
4. 크기가 N인 도미노 세트는 각 칸의 점의 개수가 N보다 작거나 같은 모든 경우를 포함하고 있다. 중복된 도미노는 없다.
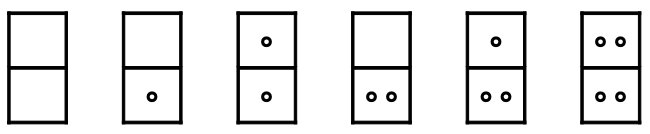
도미노 세트의 크기 N을 입력받아, 도미노 세트에 찍혀 있는 점의 개수를 출력하라.
풀이
내 풀이_1
1. n을 입력받는다.
2. 중복을 허용하지 않도록 빈 set를 선언한다.
3. 각 칸에 대해 점의 개수만큼 반복문(이중 반복문)을 돌면서, 두 수의 조합이 set에 없으면 set에 추가한다.
4. set에 저장된 점의 개수를 모두 더해 출력한다.
코드
import sys
n = int(sys.stdin.readline())
s = set()
for i in range(n + 1):
for j in range(n + 1):
if (j, i) not in s:
s.add((i, j))
sum = 0
for i, j in s:
sum += i
sum += j
print(sum)
실행 결과
아래는 set의 값도 출력한 결과다.

도미노 세트를 직접 구현한 것과 같은데, 모든 경우의 수를 다 따지기 때문에 효율적이라고 할 수는 없다.
내 풀이_2
풀이 1을 개선해보자.
- 풀이 1의 수행을 따져보면 튜플의 두 번째 원소가 i 이하일 때는 set에 추가하지 않는 점을 발견할 수 있다. 따라서 j의 반복을 i+1부터 n까지 수행하도록 수정하면 반복 횟수를 줄일 수 있다.
- set를 선언하지 않고, 바로 i와 j의 값을 sum에 더하면 수행에 필요한 메모리 공간을 줄일 수 있다.
개선점을 반영한 코드는 아래와 같다.
코드
import sys
n = int(sys.stdin.readline())
sum = 0
for i in range(n + 1):
for j in range(i, n + 1):
sum += i + j
print(sum)
실행 결과
마찬가지로 반복문 내에서 i, j의 값도 출력한 결과다.
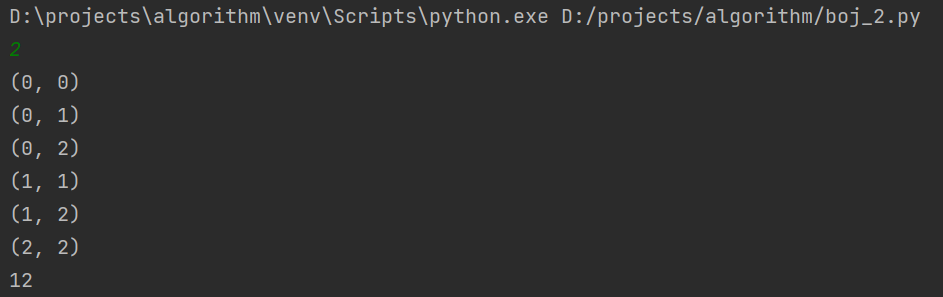
풀이 1과 동일한 결과임을 알 수 있다.
다른 풀이
수학적으로 접근하여 도미노 세트의 크기(N)와 도미노 세트의 점의 개수 간의 규칙을 찾으면 반복문도 사용하지 않고 문제를 해결할 수 있다.
고등 수학 수준이니 기억을 잘 되살려보자😅…….
도미노 세트의 크기가 1, 2, 3일 경우의 도미노 세트, 점의 개수를 정리하면 아래 표와 같다.
| 도미노 세트의 크기 | 도미노 세트 | 점의 개수 |
| 1 | (0, 0) (0, 1), (1, 1) | 1 + 2 |
| 2 | (0, 0) (0, 1), (1, 1), (0, 2), (1, 2), (2, 2) | 1 + 2 + 2 + 3 + 4 |
| 3 | (0, 0) (0, 1), (1, 1), (0, 2), (1, 2), (2, 2), (0, 3), (1, 3), (2, 3), (3, 3) | 1 + 2 + 2 + 3 + 4 + 3 + 4 + 5 + 6 |
| n | n-1의 도미노 세트 + (0~n, n) | n - 1일 때의 점의 개수 + n + (n + 1) + (n + 2) + ... + (n + n) |
즉, 정리하면 세트의 크기가 n일 때의 점의 개수는 n - 1일 때의 점의 개수와 n부터 2n까지의 합이라고 할 수 있다. 이것을 고급스럽게 수학적으로 표현하면 아래와 같다.
$$ \sum_{t=1}^n \sum_{k=t}^{2t} k$$
식을 정리해보자.
$$ \begin{matrix} \sum_{1}^n \sum_{t}^{2t} k &=& \sum_{1}^n(\sum_{t}^{2t} k - \sum_{1}^{t-1} k) \\ &=& \sum_{1}^n(\frac {2t(2t+1)} {2} - \frac {t(t-1)} {2}) &=& \sum_{1}^n(\frac {4t^2+2t-t^2+t)} {2}) \\ &=& \sum_{1}^n(\frac {3t^2+3t)} {2}) &=& \frac {3} {2} \sum_{1}^{n} (t^2 + t) \\ &=& \frac {3} {2}(\frac {n(n+1)(2n+1)} {6} + \frac {n(n+1)} {2}) &=& \frac {3} {2}(\frac {n(n+1)(2n+1)} {6} + \frac {3n(n+1)} {6}) \\ &=& \frac {3n(n+1)} {2} \frac {2n+1+3} {6} &=& \frac {n(n+1)} {2} \frac {2n+4} {2} \\ &=& \frac {n(n+1)(n+2)} {2} \end{matrix} $$
즉, 이 문제는 n을 입력받아 \(\frac {n(n+1)(n+2)} {2}\)을 계산해 출력하면 해결할 수 있다.
코드
import sys
n = int(sys.stdin.readline())
print(n * (n + 1) * (n + 2) // 2)
실행 결과

고등학교 수학 어렵다…….😵