[Algorithm] 에라토스테네스의 체

에라토스테네스의 체

고대 그리스 수학자 에라토스테네스가 발견한 소수를 찾는 방법

 

 

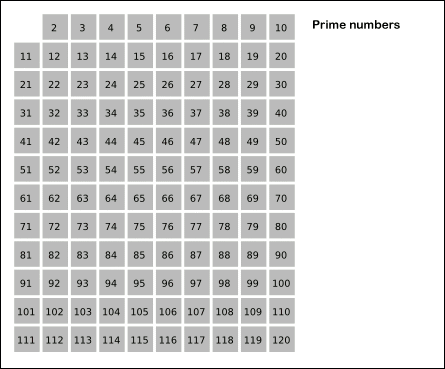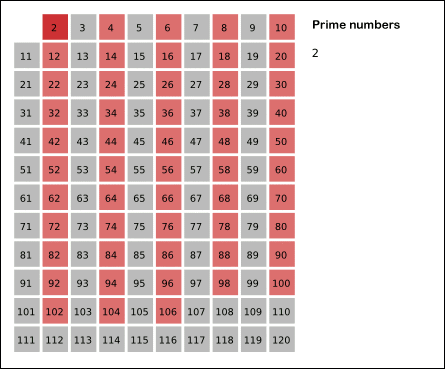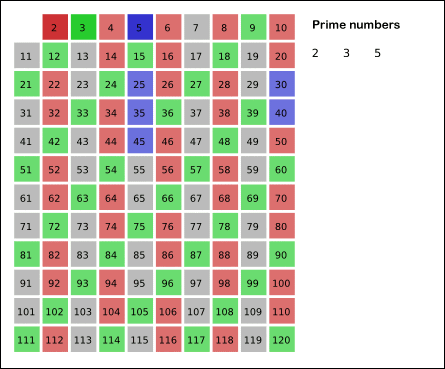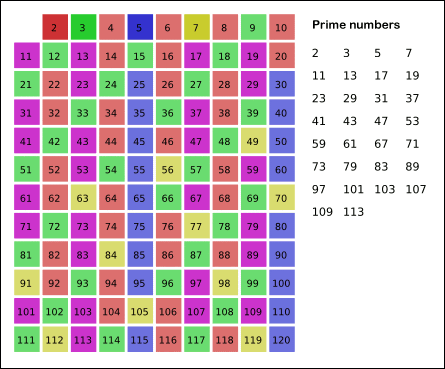
알고리즘

1. 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 즉, 2부터 n까지의 모든 수를 나열한다.
2. 지우지 않은 수 중 가장 작은 수를 찾는다. 이 수는 소수이다.
3. 자기 자신을 제외한 소수의 배수를 모두 지운다.
4. 더 지울 수가 없을 때까지 2 ~ 3 과정을 반복한다.

또는

\( \sqrt{n} \)의 정수부보다 작은 소수의 배수를 지우고 남는 수는 모두 소수이다.

그림의 경우, \( 11^2 > 120 \)이므로, 120보다 작거나 같은 수 가운데 2, 3, 5, 7의 배수를 지우고 남는 수는 모두 소수이다.

 

구현

Python으로는 아래와 같이 구현할 수 있다.

def prime_list(n):
    # 에라토스테네스의 체 초기화: n개 요소에 True 설정(소수로 간주)
    sieve = [True] * (n + 1)

    # n의 최대 약수가 sqrt(n) 이하이므로 i=sqrt(n)까지 검사
    m = int(n ** 0.5)
    for i in range(2, m + 1):
        if sieve[i]:           # i가 소수인 경우
            for j in range(i+i, n + 1, i): # i이후 i의 배수들을 False 판정
                sieve[j] = False

    # 소수 목록 산출
    return [i for i in range(2, n + 1) if sieve[i]]

 

n = 120인 경우의 실행 결과

 

참고 문서

에라토스테네스의 체