[알고리즘] 어떤 수의 모든 약수 구하기

개요

수학에서 약수(divisior)란 어떤 수를 나누어 떨어지게 하는 수를 말한다.

 

알고리즘 문제를 풀다 보면 약수를 다룰 일이 많다. 보통 어떤 수의 모든 약수를 찾는다던가, 약수의 개수를 찾게 되는데 이 글에서는 어떤 수의 모든 약수를 찾는 방법을 적어둔다.

 

 

일반적인 방법

약수를 찾을 때 가장 단순하게 접근하는 방법은 반복문을 활용하는 것이다. 예로 들어 100의 모든 약수를 찾는다고 가정할 때 1부터 100까지의 모든 수에 대해 100을 나누어 떨어지게 하는 수를 찾는 것이다.

def get_divisior(num):
    result = []
    for i in range(1, num + 1):
        if num % i == 0:
            result.append(i)
    return result


if __name__ == '__main__':
    num = 100
    print(get_divisior(num))

결과는 잘 나온다. 다만 범위 내의 모든 수에 대해 연산이 이뤄지므로 O(n)의 시간 복잡도를 가진다. 값이 아주 큰 수인 경우에는 시간 초과가 발생하게 된다.

 

 

제곱근 사용

위의 방법은 20, 25, 50, 100에 대해서도 굳이 나눗셈을 수행한다.

그러면 사람이 직접 약수를 계산할 때를 한 번 생각해 보자. 20, 25, 50, 100에 대해서도 계산을 수행할까? 아마도 그렇지 않을 것이다. 20, 25, 50, 100는 각각 100을 5, 4, 2, 1로 나눈 몫이기 때문에 더 계산할 필요 없이 약수라고 판단할 수 있기 때문이다. 

그렇다면 사람은 언제 계산을 중지할까? 100에 대한 약수를 구할 때는 아마 10에서 중지할 것이다. 몫인 10이 나눈 수와 같기 때문이다.

 

즉, 사람이 어떤 수(num)의 모든 약수를 계산할 때는 다음과 같이 계산한다.

1. 어떤 수(num)에 대해 나누어 떨어지는 수와 그 몫을 약수로 한다.

2. 1의 과정을 1부터 어떤 수(num)의 제곱근까지 반복한다.

 

코드로 표현해보면 다음과 같다. 약수 목록인 result는 중복값 제거를 위해 set으로 선언했다가 return 할 때 정렬 및 list로 변환한다.

def get_divisior_v2(num):
    result = set()
    for i in range(1, int(num ** 0.5) + 1):
        if num % i == 0:
            result.add(i)
            result.add(num // i)
    return sorted(list(result))

 

위의 결과와 비교하면 다음과 같다.

rum의 값을 1000000으로 하여 각 방법의 실행 소요 시간을 비교하자.

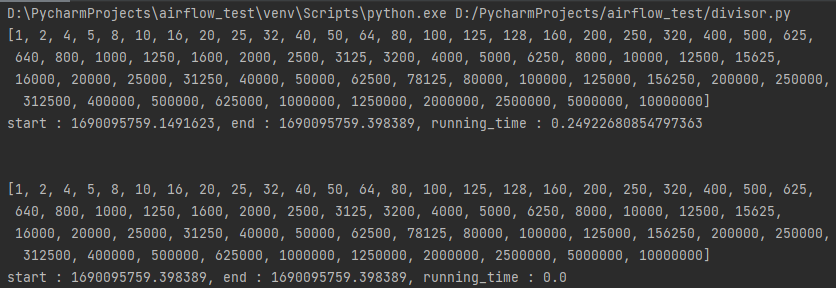
처음 방법은 0.2초가, 두 번째 방법은 0초가 소요됨으로써 소요시간에 차이가 발생하는 것을 확인할 수 있다.

 

 

참고 문서

https://mine-it-record.tistory.com/522

https://kbw1101.tistory.com/32