[백준] 2193 - 이친수
문제
문제 : https://www.acmicpc.net/problem/2193
이진수란 0과 1로만 이루어진 수를 말한다. 그중 0으로 시작하지 않으면서 1이 두 번 연속 나타나지 않는 수(1, 10, 100, 101)를 이친수(pinary number)라고 한다. 0010101, 101101은 0으로 시작하거나 1이 연속으로 나타나므로 이친수가 아니다.
수의 길이를 입력받아 해당 길이의 이친수의 개수를 구하여라.
접근
2024.04.04 - [백준] 11057 - 오르막 수와 비슷한 면이 있는데, 마지막 자리의 값에 따라 다음에 올 수 있는 수가 정해져 있다는 점이 특징이다. 1이 연속으로 나올 수 없다는 이친수의 성질을 만족해야 하기 때문이다. 따라서 숫자가 1로 끝나면 다음 길이의 이친수는 0으로 끝나고, 숫자가 0으로 끝나면 다음 길이의 이친수는 0 또는 1로 끝나게 된다.
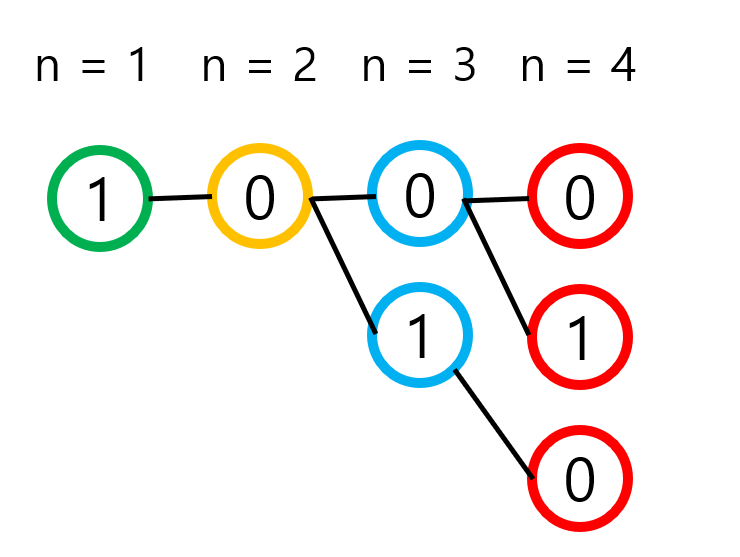
즉, 수의 길이와 마지막 자리값에 따른 수의 개수를 테이블로 표현하면 다음과 같다.
| 0 | 1 | 이친수 | |
| n = 1 | 0 | 1 | 1 |
| n = 2 | 1 | 0 | 10 |
| n = 3 | 1 + 0 | 1 | 100, 101 |
| n = 4 | 1 + 1 | 1 | 1000, 1001, 1010 |
| n = 5 | 2 + 1 | 2 | 10000, 10001, 10010, 10100. 10101, |
| n = 6 | 3 + 2 | 3 | 100000, 100001, 100010, 100100, 100101, 101000, 101001, 101010 |
위 테이블을 사용해 문제를 풀어낸다.
풀이
1. 수의 길이 및 테이블 초기화
테이블에는 마지막 자리값이 인덱스이고, 마지막 자리 값이 인덱스에 해당하는 수의 개수를 저장할 수 있도록 초기화한다.
N = int(sys.stdin.readline())
dp = [[0, 1]]
2. 테이블 업데이트
마지막 자리의 값이 0인 수의 개수는 직전 이친수의 마지막 자리값이 0인 개수와 1인 개수의 합이다.
그리고 마지막 자리의 값이 1인 수의 개수는 직전 이친수의 마지막 자리값이 0인 개수인 수와 동일하다.
자리의 값과 인덱스가 동일하게 테이블을 업데이트한다.
for i in range(1, N):
dp.append([dp[-1][0] + dp[-1][1], dp[-1][0]])
3. 결과 출력
입력으로 받은 길이의 이친수의 개수를 구해야 하므로 마지막 테이블 원소의 합을 출력한다.
print(sum(dp[-1]))
전체 소스는 아래와 같다.
import sys
N = int(sys.stdin.readline())
dp = [[0, 1]]
for i in range(1, N):
dp.append([dp[-1][0] + dp[-1][1], dp[-1][0]])
print(sum(dp[-1]))
참고 문서
https://www.acmicpc.net/problem/2193